What is K-means Clustering

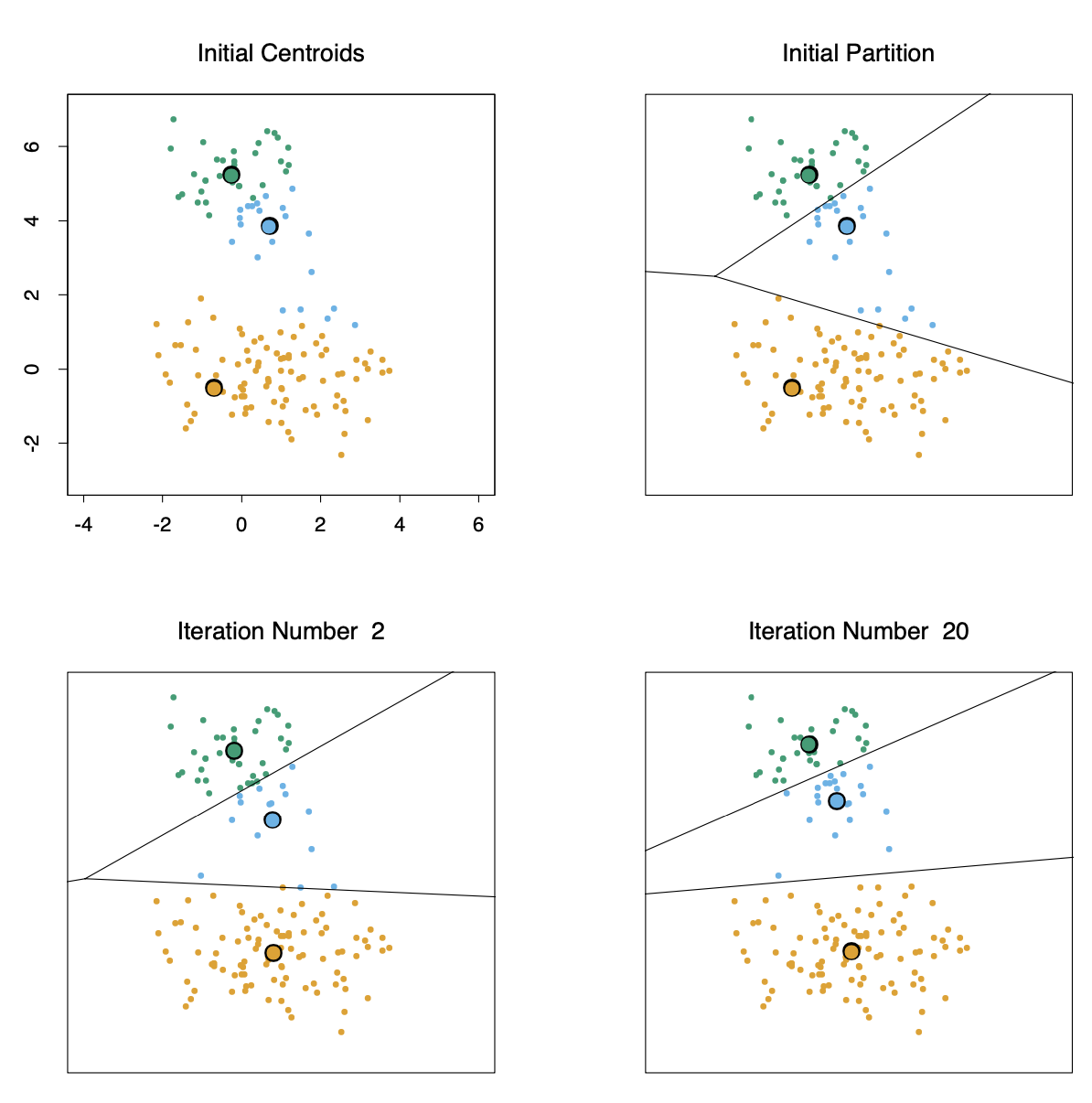
The k-Means algorithm is one of the most popular iterative descent clustering methods and the unsupervised learning’ algorithm. K stands for clustering which assigns data points to one of the K clusters based on the distance from the cluster center. Start by randomly assigning the cluster center to the space. Each data point is then assigned to one of the clusters based on the distance from the cluster center. Assign each point to one of the clusters and assign a new cluster center. This process runs repeatedly until a good cluster is found. Should assign points to one of the groups assuming that the number of clusters is given in advance in the analysis.
It aim for situations where all variables are quantitative types, and select Euclidean distance squared as a measure of dissimilarity.

\[d(x_{i}, x_{i'}) = \sum_{j=1}^{p} {(x_{ij} - x_{i'j})^2} = \|\|{x_{i} - x_{i'}}\|\|^2\]

In some cases, K is not clearly defined, and we have to think about the optimal number of K. K means clustering performs best when data is well separated. When data points overlap, this clustering is not suitable. To get help defining the K, we can use the ‘Silhouette score’ or the ‘Elbow method’ The criterion is minimized by allocating N observations to K clusters in such a way that the average difference from the cluster mean defined by the points of theat cluster within each cluster is minimized.

• Unsupervised Learning: Uses machine learning to analyze unlabeled datasets to discover patterns without human supervision.

Goal of Clustering

The goal of clustering is to divide a population or set of data points into groups so that data points within each group are more similar to each other and differ from data points within other groups. Clusters are essentially grouping objects according to how similar and different they are from each other and discover underlying patterns or structures within the data.

Algorithm

1. For a given cluster assignment \(C\), the total cluster variance, \(\min_{C, {m_{k}}_{1}^{K}} {\sum_{k=1}^{K} {N_{k}} \sum_{C(i)=k} {\|\|x_i - m_k\|\|^2}}\), is minimized with respect to \({m_1, \cdots, m_K}\) yiedling the means of the currently assigned clusters, \(\bar{x*S} = \argmin*{m} {\sum\_{i \in S} {\|\|x_i - m\|\|^2}}\).
2. Given a current set of means \({m*{1}, \cdots, m*{K}}\), \(\min*{C, {m*{k}}_{1}^{K}} {\sum_{k=1}^{K} {N*{k}} \sum* {\|\|x_i - m_k\|\|^2}}\) is minimized by assigning each observation to the closest cluster means. \(C(i) = \argmin\_1 {\|\|x_i - m_k\|\|^2}\)
3. Steps 1 and 2 are iterated until the assignments do not change.

Each of the first and second steps reduces the value of the criterion to ensure convergence. However, the results may indicate a suboptimal local minimum. In addition, start the algorithm with various random choices for the starting means, and we need to select the solution with the smallest value of the objective function.