The perceptron was investigated in 1957 by Frank Rosenblatt at Cornell. It was the first learning algorithm based on the concept of a neural network.

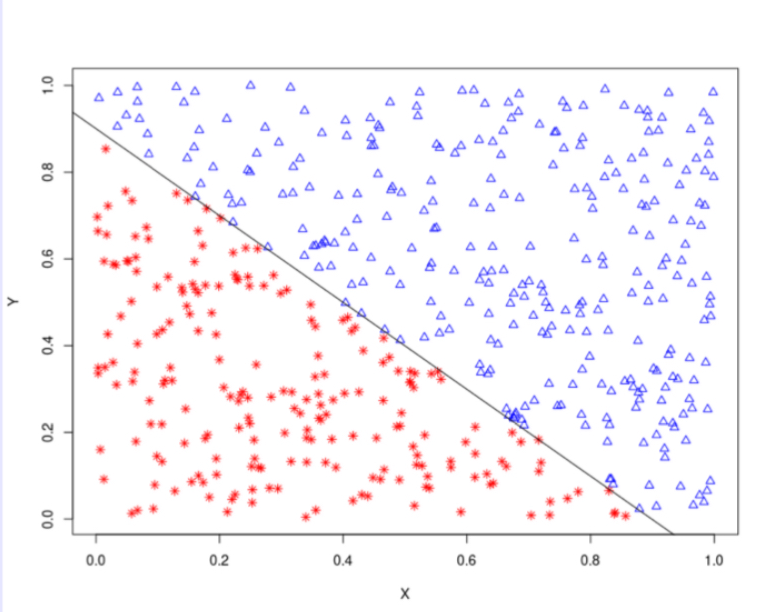
The perceptron was guaranteed to find the linear boundary between two classes if there is a boundary. The perceptron is a simple one-cell, most simplest, neural network. It is characterized as a feed-forward neural network that solves linearly separable problems. -> If the data is linearly separable, the perceptron will find the hyperplane that separates it.

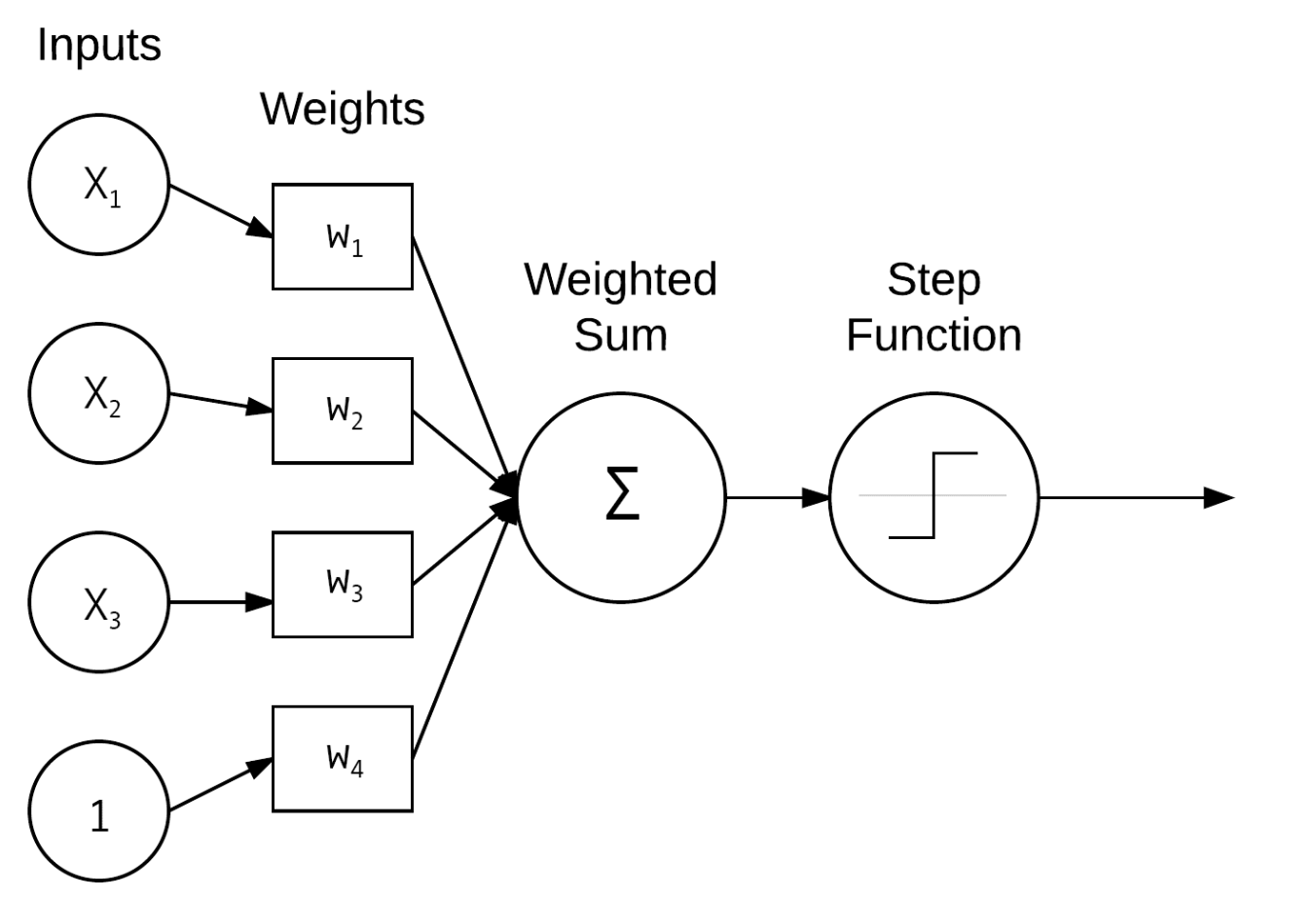
More complex neural networks can solve data mining or learning tasks more effectively by gathering several perceptrons. They work together to solve the task.

We can train a model to derive a hyperplane that will separate the classes, but there are two conditions. i) Dealing with a binary classification problem such as \(y_i \in \{-1, +1\}\) ii) Data is linearly separable.

Training is all about adjusting the weight parameter, w, until the response predicted by the perceptron becomes consistent with the true response.

However, even for binary classes, the perceptron cannot recognize the XOR function. To solve this, we need the multiple perceptron model. This is a general neural network.

Example

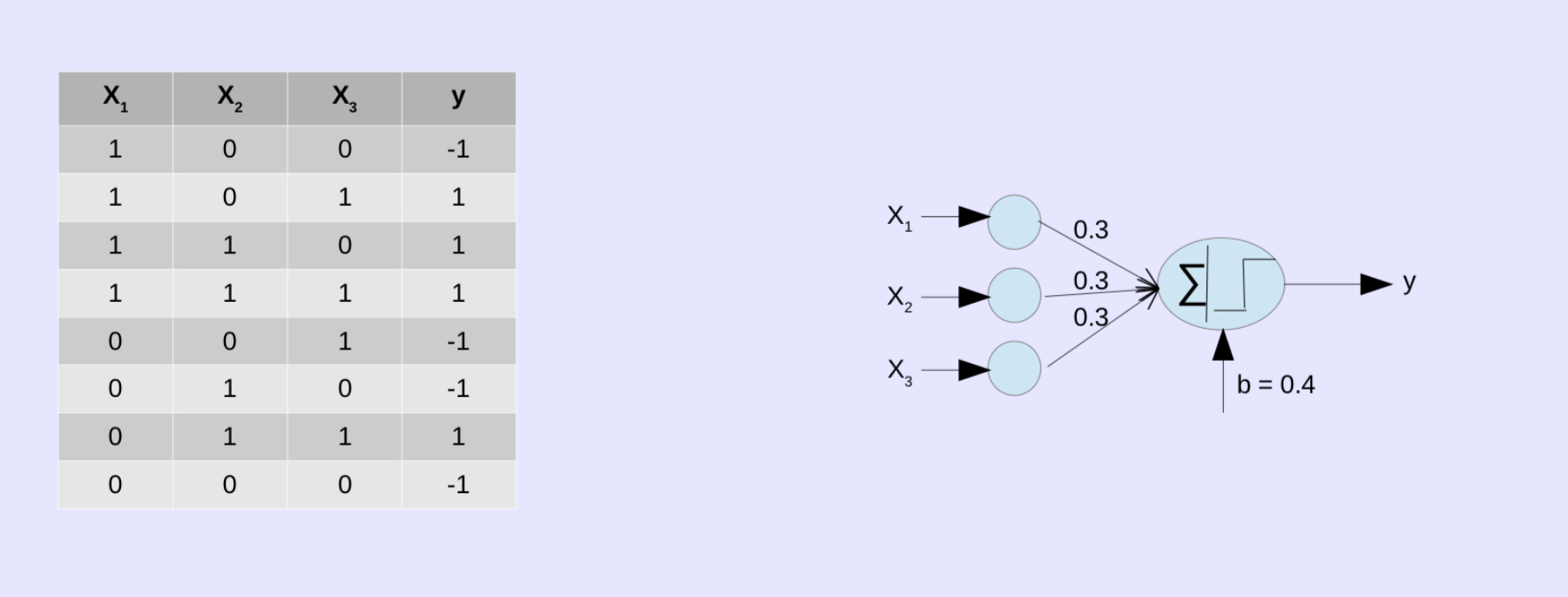
In this case, 0.3 is weight, and 0.4 is bias. We can write it as a formula, \(\hat{y} = \begin{cases} 1: 0.3x_1 + 0.3x_2 + 0.3x_3 + 0.4 \ge 0 \\ -1: 0.3x_1 + 0.3x_2 + 0.3x_3 + 0.4 < 0 \end{cases}\) This could be rewritten as \(\begin{align} \hat{y} &= sign((\sum*{i=i}^{n}{w_i x_i}) + b) \\ &= sign (\sum*{i = 0}^{n} {w_i \times x_i}) \\ &= sign(w_i \cdot x_i) \end{align}\)

Note: \(sign(x) := \begin{cases} -1 \;\;\; if \;\; x < 0, \\ 0 \;\;\;\;\;\; if \;\; x = 0, \\ 1 \;\;\;\;\;\; if \;\; x > 0 \end{cases}\)

Reference

• CS 422, Data Mining, prof. Vijay K. Gurbani, Fall 2023, Illinois Institute of Technology