A dynamic table T is an array with changeable length. When the array is full, we increase its length; when the array is “Too empty”, we reduce its length.

The claim that hash tables give have \(O(1)\) performance for lookup and the insert is based on the assumption that the number of elements stored in the table is comparable to the number of buckets. If a hash table has many more elements than buckets, the number of elements stored in each bucket will become large. 불필요한 사용을 막는다.

Attributes

• T.table : the array itself
• T.size : length of the array
• T.num : number of elements in T Start with \(T.size = 0\) and \(T.num = 0\)

Insertion

Start with \(T.table\) being empty. When inserting into an empty table, expand \(T.table\) so that \(T.size = 1\), then insert the element. Later, whenever need to insert an element into a full table, (\(T.size = T.num\)), expand \(T.table\) so that \(T.size\) is doubled. To double the size of $T.table$, claim a new empty array of doubled size, and move all the elements into the new array.

Aggregate analysis

Let \(c_i\) be the actual cost of the \(i^{th}\) insertion. If \(T.table\) still have available slots while the \(i^{th}\) insertion, then \(c_i = 1\); if \(T.table\) is full while the \(i^{th}\) insertion and \(T.size = m\), then \(c_i = m + 1\). If there are n insertions, the total cost of n operations is below. -Note: do not consider the following. - There is only one table expansion, and \(T.size = m >> n\). In this case, there are not enough operations to be an amortized analysis. - Thus, assume that during all n insertions, \(T.size = m\) can be at most \(O(n)\). With the note above, can see that n operations have a total cost \(O(n^2)\), but this upper bound is not tight.

Total cost of n insertions

There are two parts. One is i) n simple insertions and ii) some table expansions.

i) n simple insertions

 It needs n times.

ii) Some table expansions

Assume that we have a worst-case. Start \(T.table\) being full and \(T.size = m\) So we start with a table expansion immediately and have a table expansion in the last insertion. A table expansion immediately takes \(m\) time then after another \(m\) insertions we need another table expansion that takes \(2m\) time. After another \(2m\) insertions we need another table expansion that takes \(4m\) time, and so on. In the end, after another \(2^km\) time. \(n = 1 + m + 2m + \cdots + 2^km\), and the total cost of table expansion is \(m + 2m + 4m + \cdots + 2^{k+1}m\). \(m + 2m + 4m + \cdots + 2^{k+1}m = (m - 2) + (2 + 2m + 4m+ \cdots + 2^{k+1}m)\) \(= (m -2) + 2n\) Thus, the total cost of \(n\) insertions are at most \((m - 2) + 2n + n = 3n + m -2\). \(m = O(n)\), so the total cost is \(O(n)\).

When \(m = 0\) (start with \(T.size = 0\)) or when $n$ is large enough (\(n >> m\)), have this total cost equals \(3n\). Thus, the amortized cost for insertion is \(\frac{3n}{n} = 3\).

Accounting Method

Whenever we do a simple insertion, we put two extra coins on that spot. When the array is full, \(T.num = T.size = 2m\), each of the \(m\) spots contain 2 coins, so we can use these \(2m\) coins to move all \(2m\) elements into a new table of size \(4m\) for free. Thus, the amortized cost for insertion is 3.

Potential Method

Define \(\Phi(T) = 2T.num - T.size\)
-> always non-negative

At first $$T.num = T.size = 0$$. After any number of insertions, we always have $$T.table$$ is at least **half full** so $$2\cdot T.num \ge T.size$$ is always true.

Let \(T_i\) be the dynamic table after the \(i^{th}\) insertion and simplify \(\Phi(T_i)\) as \(\Phi_i\).

\(c_i\) is simple insertion

\(\hat {c_i} = c_i + \Phi_i - \Phi_{i-1}\) \(= 1 + (2\cdot T_i.num - T_i.size) - (2\cdot T_{i-1}.num - T_{i-1}.size)\) \(= 1 + 2\cdot (T-i.num - T_{i-1}.num) + (T_{i-1}.size - T_i.size)\) \(= 1 + 2\cdot 1 + 0\) \(= 3\)

\(c_i\) is insertion with expansion

\(\hat{c_i} = c_i + \Phi_i - \Phi_{i-1}\) \(= (T_{i-1}.num + 1) + (2\cdot T_i.num - T_i.size) - (2\cdot T_{i-1}.num - T_{i-1}.size)\)

Let \(T_{i-1}.num = m\), then \(T_{i-1}.size = m, T_i.size = 2m, T_i.num = m + 1\) : \(\hat{c_i} = (m + 1) + (2\cdot(m + 1) - 2m) - (2\cdot m - m)\) \(= (m + 1) + 2 - m\) \(= 3\)

Insertion and Deletion

What about we contract the table so that \(T.size\) is halved whenever we delete from a half-full table?

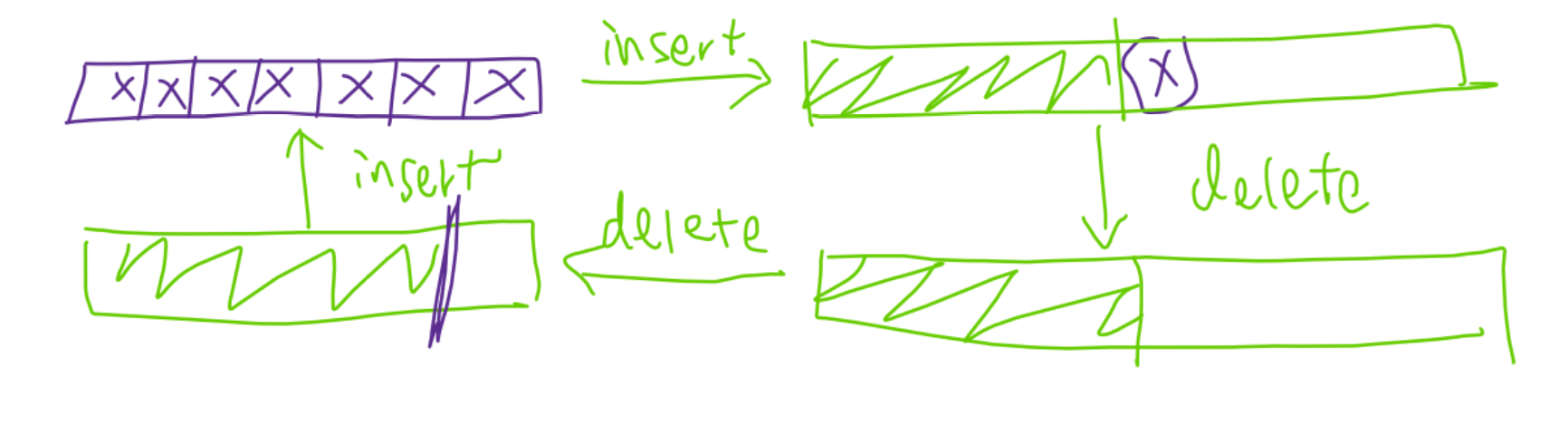
If we contract whenever it is half-full, we can have a series of operations that half of them with \(\Theta (n)\) time, and the total cost will be \(\Theta(n^2)\), making the amortized cost of each operation \(\Theta(n)\).

Change the contraction strategy to whenever delete from a 1/4 full table, contract the table so that \(T.size\) is halved. Then we need a new potential function, since \(T\) can be less than half-full and \(\Phi(T) = 2\cdot T.num - T.size\) can be less than 0.

Let \(\alpha(T) = \frac{T.num}{T.size}\) represents how full \(T.table\) is. When \(T.num = T.size = 0\), define \(\alpha(T) = 1\). The following is a new potential function: \(\Phi(T) =\) \(\begin{cases} 2\cdot T.num - T.size, \; if\; \alpha(T) \ge \frac{1}{2} \\ \frac {T.size}{2} - T.num, \; if\; \alpha(T) < \frac{1}{2} \end{cases}\)

With this new potential function, let us analyze a sequence of \(n\) insertion and deletion operations.

Consider the case that the \(i^{th}\) operation is an insertion

There are two cases.

When \(\alpha(T_{i-1}) < \frac{1}{2}\) and …

any insertion won’t trigger a table expansion.

if \(\alpha T(_i) < \frac{1}{2})\)

\[\begin{aligned}\hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= 1 + (\frac{T_i.size}{2} - T_i.num) - (\frac{T_{i-1}.size}{2} - T_{i-1}.num)\\ &= 1 + (\frac{T_i.size}{2} - \frac{T_{i-1}.size}{2}) + (T_{i-1}.num - T_i.num)\\ &= 1 + 0 + (-1) = 0 \end{aligned}\]

but \(\alpha (T_i) \ge \frac{1}{2}\)

\[\begin{aligned} \hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= 1 + (2\cdot T_i.num - T_i.size) - (\frac{T_{i-1}.size}{2} - T_{i-1}.num)\\ &= 1 + (2\cdot (T_{i-1}.num + 1) - T_{i-1}.size) - (\frac{T_{i-1}.size}{2} - T_{i-1}.num)\\ &= 3\cdot T_{i-1}.num - \frac{3}{2}T_{i-1}.size) + 3\\ &= 3\cdot \alpha(T_{i-1})\cdot T_{i-1}.size -\frac{3}{2}T_{i-1}.size + 3\\ &< \frac{3}{2}T_{i-1}.size - \frac{3}{2}T_{i-1}.size + 3\\ & = 3 \end{aligned}\]

Consider the case that the $i^{th}$ operation is deletion

There are four cases.

When \(\alpha(T_{i-1}) \ge \frac{1}{2}\)

and \(\alpha(T_i) \ge \frac{1}{2}\)

-> Before and after deletion, the table is at least half full.

\[\begin{aligned} \hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= 1 + (2\cdot T_i.num - T_i.size) - (2\cdot T_{i-1}.num - T_{i-1}.size)\\ &= 1 + 2\cdot (T_i.num - T_{i-1}.num) + (T_{i-1}.size - T_i.size)\\ &= 1 + (-2) + 0 = -1 \end{aligned}\]

but \(\alpha(T_i) < \frac{1}{2}\)

-> Before deletion, the table was at least half full and after deletion, the table is less than half.

\[\begin{aligned} \hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= 1 + (\frac{T_i.size}{2} - T_i.num) - (2\cdot T_{i-1}.num - T_{i-1}.size)\\ &= 1 + (\frac{T_{i-1}.size}{2} - (T_{i-1}.num -1)) - (2\cdot T_{i-1}.num - T_{i-1}.size)\\ &= -3T_{i-1}.num + \frac{3}{2}T_{i-1}.size + 2\\ &= -3\cdot \alpha(T_{i-1})\cdot T_{i-1}.size + \frac{3}{2} T_{i-1}.size + 2\\ &\le -\frac{3}{2}T_{i-1}.size + \frac{3}{2}T_{i-1}.size + 2\\ &= 2 \end{aligned}\]

When \(\alpha (T_{i-1}) < \frac{1}{2}\)

Simple deletion

\[\begin{aligned} \hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= 1 + (\frac{T_i.size}{2} - T_i.num) - (\frac{T_{i-1}.size}{2} - T_{i-1}.num)\\ &= 1 + (\frac{T_i.size}{2} - \frac{T_{i-1}.size}{2}) + (T_{i-1}.num - T_i.num)\\ &= 1 + 0 + 1 = 2 \end{aligned}\]

deletion with table contraction

\[\begin{aligned} \hat{c_i} &= c_i + \Phi_i - \Phi_{i-1}\\ &= (1 + T_i.num) + (\frac{T_i.size}{2} - T_i.num) - (\frac{T_{i-1}.size}{2} - T_{i-1}.num) \end{aligned}\]

Let $T_i.num = m - 1$, then $T_i.size = 2m, T_{i-1}.size = 4m, T_{i-1}.num = m$

\[\begin{aligned} \hat{c_i} &= (1 + m -1) + (m - m + 1) - (2m - m)\\ &= m + 1 = 1 \end{aligned}\]

Reference

• CS 430, Introduction to Algorithm, prof. Wang, Xiaolang, Spring 2023, Illinois Institute of Technology